LR 与 Sigmoid
Table of Contents
本文目的
LR 也就是 Logistic Regression,但是在学习的过程中,有些不解的疑惑。 下面的内容就是这篇文章的主要内容:
- 为什么有了 Linear Regression, 又会出现一个 Logistic Regression?
- Logistic Regression 明明是一个回归模型,为什么会用于分类?
- Logistic Regression 叫法的由来是什么?
- 关于 LR 中使用为什么使用 Sigmoid 函数,而不是其他的?
Logistic Function
Logistic Function(Logistic Curve) 是下面的这种形式: \[{\displaystyle f(x)={\frac {L}{1+e^{-k(x-x_{0})}}}}\]
其中的 x0, L, k 会决定这个函数的形式,当 x0=0, L=1, k=1 时就是我们常见的 Sigmoid 函数了:
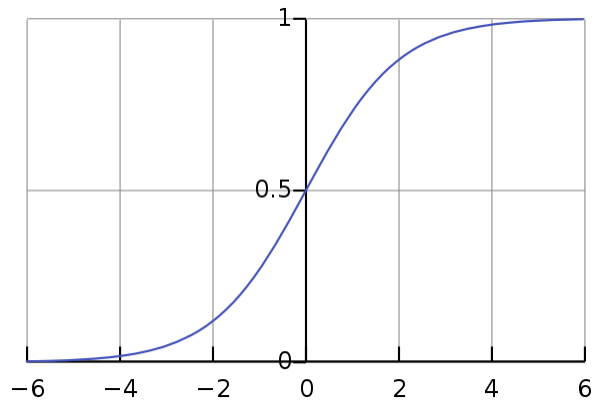
我们可以在 WolframAlpha 上调戏一下这个公式。
关于“为什么叫 Logistic Regression?”这个问题就不言而明了,正是因为它使用了 Logistic Function,所以才有了 Logistic Regression 这个名字。
但是问题又来了,为什么会使用 Sigmoid 函数也就是 Logistic Function 呢?
Logistic Regression 回归模型
在机器学习中,我们用 Logistic Regression 来进行分类问题的处理,一般是处理二分类问题,其实它还可以处理多分类的问题。
既然是处理模型的分类问题,为什么还叫 Regression 呢?其实,它就是一个回归模型,我们看 Logistic Function 应该也明白了,它的输出 Y 是一个概率。只是碰巧我们可以拿它来进行分类的处理。
LR 与 Sigmoid
现在就出现一个重要的问题,“为什么 LR 会使用 Sigmoid,而不是其他的函数?”。
其实这个问题本身就是不对的,前面解释了正是因为 Sigmoid 才有了 LR, 而不是 LR 选择了 Sigmoid。所以这里的本质问题是:为什么使用线性模型进行回归学习要使用 基于 Sigmoid 的 LR,而不是其他的 Regression。如果我们能够找到一个函数 F ,也能达到下面的功能的话,是不是也可以用 F Regression 呢? \[\begin{equation} H(x)={\begin{cases}0,&x<0\\{\frac{1}{2}},&x=0\\1,&x>0\end{cases}}\tag {1} \end{equation}\]
到这里会出现一个新的概念: 广义线性模型(GLM)。如何使用线性模型进行分类任务?我们可以在广义线性模型中找到答案:找到一个单调可微的函数将分类认为的真实标记 y 与线性回归模型(w*x + b)的到的预测值联系起来,也就是使用一个(link function)。这里也解释了为什么公式 (1) 无法使用。
现在的一个关键就是这个 link function 是什么呢? 事实情况是这里的 link function 有三个,我们可以在 Links Function 了解一下。 这个解释了为什么我们会选择使用 sigmoid function, 也就是 logit link function。关于一个分布对应什么样的 link function,是有一些条件的, 具体可以看 广义线性模型 。
最终,关于最初的疑问其实是历史的选择,我们可以选择其他的 regression 来做这个问题,但是这里是有好坏之分的。这也是为什么选择 Sigmoid 的原因。 它有如下的优点:
- sigmoid 函数连续,单调递增
- 对 sigmoid 函数求导非常的方便
\[S(t)={\frac {1}{1+e^{-t}}}.\]
\[{\displaystyle S'(t)=S(t)(1-S(t)).}\]
缺点:
这里主要看应用场景了,如果在深度学习中,它相比于 ReLU 确实是不好的。
- sigmoid 函数反向传播时,很容易就会出现梯度消失的情况
- sigmoid 作为激活函数计算量大(指数运算)